Вчені з університетів Падерборна та Левена вирішують давно відому задачу математики. Творіть історію за допомогою 42 цифр: вчені з Університету Падерборна та KU Leuven розкрили десятирічну таємницю математики за допомогою так званого дев’ятого числа Дедекінда. Експерти з усього світу шукали це значення з 1991 року. Вчені з Падерборна дійшли до точної послідовності чисел за допомогою розташованого там суперкомп’ютера Noctua. Результати будуть представлені у вересні на Міжнародному семінарі з булевих функцій та їх застосування (BFA) у Норвегії.
Те, що розпочалося як магістерська робота Леннарта Ван Гіртума, тоді студента інформатики в KU Leuven, а нині наукового співробітника Університету Падерборна, стало величезним успіхом. Учені приєдналися до видатної групи своєю роботою: більш ранні числа в серії були знайдені самим математиком Річардом Дедекіндом, коли він визначив проблему в 1897 році, а пізніше великими діячами ранньої інформатики, такими як Рендольф Черч і Морган Ворд. «Протягом 32 років розрахунок D(9) був відкритим викликом, і було сумнівно, чи буде взагалі можливо обчислити це число», — каже Ван Гіртум.
Попереднє число в послідовності Дедекінда, 8-е число Дедекінда, було знайдено в 1991 році за допомогою Cray 2, найпотужнішого суперкомп’ютера на той час. «Тому нам здавалося можливим, що вже зараз можна обчислити 9-те число на великому суперкомп’ютері», – говорить Ван Гіртум, описуючи мотивацію амбітного проєкту, який він спочатку реалізував спільно з керівниками свого магістра. дисертація в KU Leuven.
Піщинки, шахи та суперкомп’ютери
Основним предметом чисел Дедекінда є так звані монотонні булеві функції. Ван Хіртум пояснює: «По суті, монотонну булеву функцію у двох, трьох і нескінченних вимірах можна уявити як гру з n-вимірним кубом. Ви врівноважуєте куб на одному куті, а потім фарбуєте кожен кут, що залишився, білим або червоним. Є лише одне правило: ніколи не можна розміщувати білий кут над червоним. Це створює своєрідний вертикальний червоно-білий перетин. Мета гри полягає в тому, щоб порахувати, скільки є різних надрізів. Їх кількість визначається як число Дедекінда. Навіть якщо здається, що це не так, цифри швидко стають гігантськими: восьме число Дедекінда вже має 23 цифри».
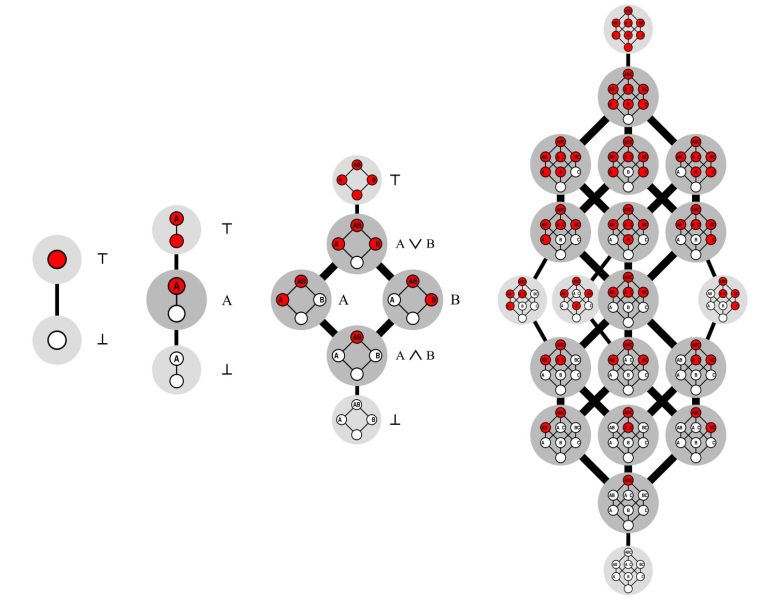
На малюнку показано всі можливі розрізи для розмірів 0, 1, 2 і 3. Кількість цих кольорових 2D, 3D, – N-вимірних розрізів, які можна сформувати, визначається як число Дедекінда. Авторство: Падерборнський університет
Порівняно великі — але незрівнянно легші для обчислення — числа відомі з легенди про винайдення гри в шахи. «Згідно з цією легендою, винахідник шахової гри попросив у короля лише кілька зерен рису на кожну клітинку шахової дошки як нагороду: одну зернину на першу клітинку, дві зернинки на другу, чотири на третю. , і вдвічі більше на кожному з наступних квадратів. Король швидко зрозумів, що це прохання неможливо виконати, адже такої кількості рису не існує в усьому світі. Кількість рисових зерен на повній дошці матиме 20 цифр — неймовірна кількість, але все одно менше, ніж D(8). Коли ви усвідомлюєте ці порядки величин, стає очевидним, що для визначення D(9) знадобляться як ефективний обчислювальний метод, так і дуже швидкий комп’ютер», — сказав Ван Гіртум.
Щоб обчислити D(9), вчені використали методику, розроблену керівником магістерської роботи Патріком Де Каусмакером, відому як формула P-коефіцієнта. Він дає можливість обчислити числа Дедекінда не підрахунком, а дуже великою сумою. Це дозволяє декодувати D(8) всього за вісім хвилин на звичайному ноутбуці. Але те, що займає вісім хвилин для D(8), перетворюється на сотні тисяч років для D(9). Навіть якщо ви використовуєте великий суперкомп’ютер виключно для цього завдання, все одно знадобляться багато років, щоб завершити обчислення», – зазначає Ван Гіртум. Основна проблема полягає в тому, що кількість членів у цій формулі неймовірно швидко зростає. «У нашому випадку, використовуючи симетрії у формулі, ми змогли зменшити кількість членів до «лише» 5,5*10^18 — величезної кількості. Для порівняння, кількість піщинок на Землі становить приблизно 7,5*10^18, на що чхати нема чого, але для сучасного суперкомп’ютера 5,5*10^18 операцій цілком посильні», — зазначив комп’ютерник. Проблема: обчислення цих термінів на звичайних процесорах є повільним, а також використання графічних процесорів як на цей час найшвидшої технології апаратного прискорення для багатьох програм ШІ неефективно для цього алгоритму.
Рішення: спеціальне апаратне забезпечення з використанням вузькоспеціалізованих і паралельних арифметичних пристроїв — так званих FPGA (програмованих вентильних матриць). Ван Хіртум розробив початковий прототип апаратного прискорювача та почав шукати суперкомп’ютер, який мав би необхідні карти FPGA. Під час цього він дізнався про комп’ютер Noctua 2 у «Падерборнському центрі паралельних обчислень (PC2)» в Університеті Падерборна, який має одну з найпотужніших у світі систем FPGA.
Професор доктор Крістіан Плессл, голова PC2, пояснює: «Коли Леннарт Ван Гіртум і Патрік Де Коусмакер зв’язалися з нами, нам одразу стало зрозуміло, що ми хочемо підтримати цей проєкт зйомки з Місяця. Розв’язання комбінаторних проблем за допомогою ПЛІС є багатообіцяючою сферою застосування, і Noctua 2 є одним із небагатьох суперкомп’ютерів у світі, з яким експеримент взагалі можливий. Надзвичайні вимоги до надійності та стабільності також становлять виклик і випробування для нашої інфраструктури. Консультаційна група експертів FPGA тісно співпрацювала з Леннартом, щоб адаптувати та оптимізувати додаток для нашого середовища». Джерело
