Дедал міг чомусь навчитися від команди фізиків із Великобританії та Швейцарії. Взявши принципи фрактальної геометрії та стратегічної гри в шахи, вони створили, як вони кажуть, найдиявольськіший лабіринт, який будь-коли створювався.
Під керівництвом фізика Фелікса Флікера з Брістольського університету у Великій Британії група згенерувала маршрути, які називаються гамільтоновими циклами, у шаблонах, відомих як мозаїки Аммана-Бенкера, створюючи складні фрактальні лабіринти, які, за їх словами, описують екзотичну форму матерії, відому як квазікристали.
І все це було навіяно рухом лицаря навколо шахової дошки.
«Коли ми подивилися на форми ліній, які ми побудували, ми помітили, що вони утворюють неймовірно заплутані лабіринти. Розміри наступних лабіринтів зростають експоненціально — і їх нескінченна кількість», — пояснює Флікер.
«У турі лицаря шахова фігура (яка стрибає на дві клітинки вперед і одну праворуч) відвідує кожну клітинку шахової дошки лише один раз, перш ніж повернутися на початкову клітинку. Це приклад «Гамільтонового циклу» – циклу через карту, яка відвідує всі зупинки лише один раз».

Квазікристали є формою матерії, яка дуже рідко зустрічається в природі. Це щось на зразок дивного гібриду впорядкованих і невпорядкованих кристалів у твердих тілах.
У впорядкованому кристалі – солі, алмазів чи кварцу – атоми розташовані в дуже чіткому візерунку, який повторюється в трьох вимірах. Ви можете взяти частину цієї решітки та накласти її на іншу, і вони ідеально збігатимуться. Невпорядковане, або аморфне, тверде тіло — це те, в якому всі атоми просто химерні. До них відносяться скло та деякі форми льоду, які зазвичай не зустрічаються на Землі.
Квазікристал — це матеріал, у якому атоми утворюють візерунок, але візерунок не повторюється повністю. Це може здатися досить схожим на себе, але накладені частини візерунка не збігатимуться.
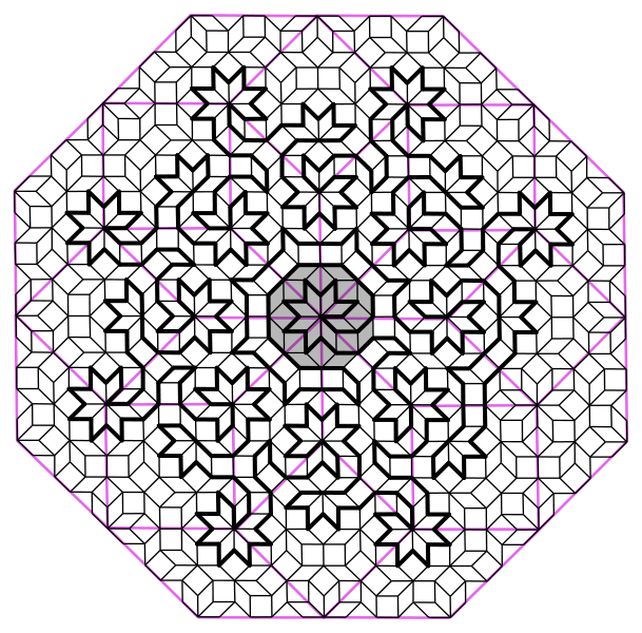
Ці схожі на вигляд, але неідентичні візерунки дуже схожі на математичну концепцію, яка називається аперіодичними мозаїками, яка включає візерунки форм, які не повторюються однаково. Одним із них є знаменита плитка Пенроуза. Черепиця Амманна-Бенкера є іншою.
Використовуючи набір двовимірних мозаїк Амманна-Бінкера, Флікер та його колеги, фізики Шобна Сінгх з Кардіфського університету у Великій Британії та Джером Ллойд з Женевського університету в Швейцарії створили гамільтонові цикли, які, за їхніми словами, описують структуру атома квазікристала. .
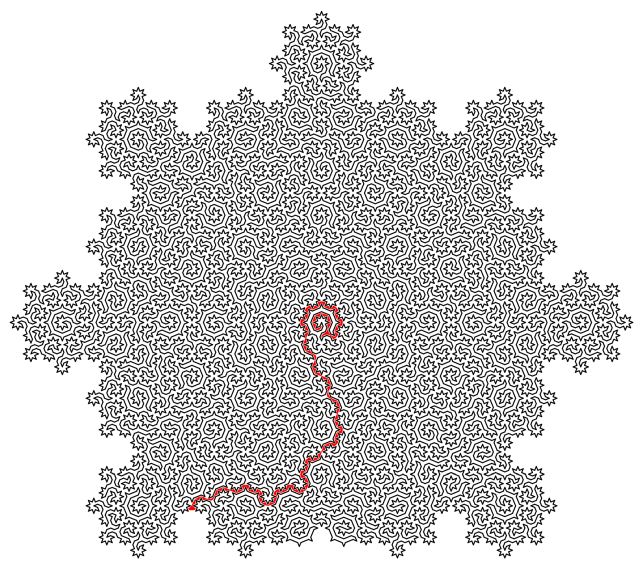
Створені ними цикли відвідують кожен атом у квазікристалі лише один раз, з’єднуючи всі атоми в одну лінію, яка ніколи не перетинає сама себе, а чітко продовжується від початку до кінця. І це можна нескінченно масштабувати, створюючи тип математичної моделі, відомої як фрактал, у якій найменші частини нагадують найбільші.
Потім ця лінія створює лабіринт із початковою точкою та виходом. Але дослідження має набагато більші наслідки, окрім розваги роздратованих дітей у закусочних. З одного боку, знайти гамільтонові цикли надзвичайно важко. Рішення, яке дозволило б ідентифікувати гамільтоніани, має потенціал для вирішення багатьох інших складних математичних проблем, від складних систем пошуку маршрутів до згортання білка.
І, що цікаво, є наслідки для захоплення вуглецю за допомогою адсорбції, промислового процесу, який передбачає перенесення молекул у рідину шляхом прилипання їх до кристалів. Якби ми могли замість цього використовувати квазікристали для цього процесу, гнучкі молекули могли б упакуватися щільніше, лежачи вздовж гамільтонового циклу в них.
«Наша робота також показує, що квазікристали можуть бути кращими за кристали для деяких застосувань адсорбції», — говорить Сінгх.
«Наприклад, гнучкі молекули знайдуть більше способів приземлитися на нерегулярно розташовані атоми квазікристалів. Квазікристали також крихкі, тобто вони легко розбиваються на крихітні зерна. Це максимізує їхню площу поверхні для адсорбції». І якщо у вас є мінотавр, який вам потрібно десь сховати, ми думаємо, що знаємо когось, хто може допомогти. Дослідження опубліковано в Physical Review X.

